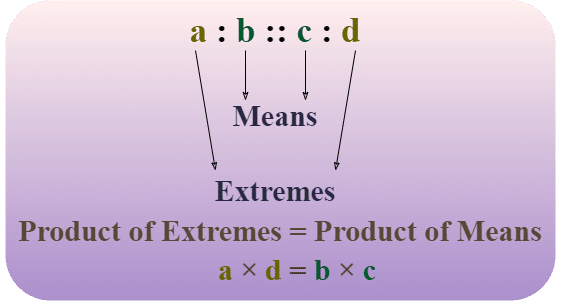What Are the Top Scoring Strategies for Ratio-Proportion Questions?

Solving numerical problems requires both speed and precision. Many candidates struggle with time-consuming calculations and complex relationships between numbers. However, those who score well approach these problems strategically. The right techniques can simplify even the toughest problems. Instead of relying on lengthy calculations, focusing on logical shortcuts and patterns can lead to quick and accurate answers. Let’s explore the most effective strategies.

Understand the Basics Before Jumping to Shortcuts

Before applying advanced techniques, mastering fundamental concepts is essential. A clear understanding of fractions, percentages, and number relationships makes problem-solving easier. The proportion of ratio in any problem must be carefully analyzed before attempting calculations.

Breaking problems into smaller parts helps in identifying patterns. Instead of solving directly, candidates should first examine how numbers relate to each other. This approach prevents common calculation errors.

Use Cross Multiplication for Quick Comparisons

Cross multiplication is a powerful technique for comparing values quickly and efficiently. It simplifies calculations, eliminates unnecessary steps, and is especially useful when working with fractions, missing values, or unknown variables. Mastering this method enhances problem-solving speed and accuracy.

• Quick Comparisons Without Conversion – Cross multiplication allows candidates to compare fractions or decimals instantly. Instead of converting values into a common denominator, multiplying diagonally helps determine relationships between numbers.
• Eliminating Trial and Error – This method reduces reliance on trial and error, providing a direct approach to solving problems. It saves time by offering a structured technique instead of guessing.
• Handling Missing Values and Variables – Cross multiplication is especially useful when dealing with equations involving unknown variables. It simplifies the process by allowing direct comparisons.
• Building Confidence Through Practice – Regular practice with different types of problems strengthens problem-solving skills. Cross-multiplication in various scenarios enhances speed, accuracy, and efficiency in competitive exams.

Apply Unitary Method for Faster Calculations

The unitary method simplifies multi-step calculations. This approach involves reducing problems to a single unit and then scaling up accordingly. By solving for one part first, candidates can quickly extend calculations to find the final answer. This technique is particularly useful for complex comparisons.

Using this method prevents confusion in word-based problems. It ensures that calculations remain structured and logical, minimizing errors. The key is to set up the problem correctly before applying the unitary approach.

Identify Patterns and Use Proportional Scaling

In many cases, problems follow a fixed pattern. Recognizing these structures allows candidates to apply direct scaling instead of solving each step manually. Multiplying or dividing by common factors speeds up the process.

Using estimation also helps. Instead of calculating exact values immediately, checking approximate differences guides problem-solving. This strategy is especially useful for multiple-choice questions where quick elimination matters.

Practice with Real-Time Constraints

Some candidates excel under pressure, while others struggle, and the difference often comes down to consistent practice. Training under timed conditions and exploring multiple problem-solving techniques help build speed, accuracy, and confidence in exams.

• Practicing Under Time Constraints – Solving problems within a fixed time frame improves speed and accuracy. Setting a timer while practicing helps simulate real exam conditions, making candidates more comfortable with time pressure.
• Enhancing Time Management Skills – Timed practice teaches candidates to allocate time wisely for each question. This prevents unnecessary delays on difficult problems and ensures efficient completion of the test.
• Exposure to Different Difficulty Levels – Practicing a range of difficulty levels builds adaptability. Regular exposure to challenging problems prepares candidates for unpredictable exam scenarios.
• Using Multiple Problem-Solving Approaches – Relying on a single method may not always be effective. Practicing with various strategies enhances problem-solving flexibility, making candidates more efficient.

Success in numerical problem-solving depends on smart strategies rather than just formulas. By focusing on core concepts, applying cross-multiplication, and recognizing patterns, candidates can solve problems quickly and accurately. For those looking to improve further, understanding the proportion of ratio in different contexts can provide deeper insights. With the right mindset and consistent practice, solving numerical problems becomes less about memorization and more about logical application. A strategic approach always leads to better results!